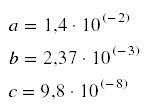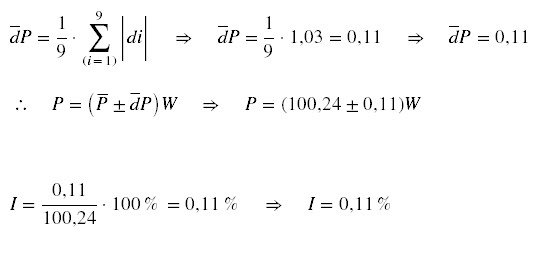Sensores de temperatura

NTC  (Negative Temperature Coeficient)

Característica do termistor do tipo NTC: À medida que se eleva a temperatura a resistência elétrica diminui.

A equação que rege o comportamento do NTC (equação de Steinhart–Hart) é:

Selecionam-se as constantes a, b e c definidas no manual do fabricante do Termistor NTC, ou através de medições realizadas em ensaio quando estas informações não estiverem disponíveis.

Como exemplo, as constantes do sensor (Termistor NTC 10K, 25ºC), que foi utilizado em aula de laboratório são:

Nota: estes valores dependem do material do NTC.

Exemplo:

1) Determinar a evolução da temperatura para o seguinte conjunto de medidas de resistência.

Aplicando a equação:

temos a evolução da temperatura.      (Utilizando, Microsoft Excel)

LM35

O LM35 é um circuito integrado sensor de Temperatura de Precisão, para graus Celsius, ele é um termômetro preciso e sensível, além de ser barato e de fácil aquisição.  Para experiência: foi comprado na Santa Ifigênia.

Faixa de medição – 55º ~ + 150 ºC com precisão de ± 0,5 ºC.  A tensão de saída é analógica e contínua: 10 mV/ºC.

Com um Multímetro, ou com uma Placa de Arduíno podemos ter um indicador de temperaturas de forma simples.

Ponte Wheatstone

A Ponte de Wheatstone é uma configuração (=montagem) que serve para descobrirmos o valor, com precisão, de uma resistência elétrica desconhecida.

Aplicações:

Medição de Resistência; Medição de Temperatura (NTC, PTC); Medição de Pressão (Strain Gauge); Medição de Peso (Strain Gauge); LDR (Light Dependent Resistor).

Desta vez vamos estudar apenas como:

• Ohmímetro de precisão (sensibilidade, reprodutividade, calibração)
• Sensor: temperatura (NTC)

Esquema elétrico de Ponte de Wheatstone:

Supondo que as quedas de tensão nos resistores R1 (VR1) e R3 (VR3) sejam iguais e que, as quedas de tensão nos resistores R2(VR2) e R4(VR4) sejam iguais, o valor da tensão é zero. 

Se R3 for desconhecida (Rx) e R4 for um potenciômetro (Rp), temos:

Desse modo, podemos ajustar o potenciômetro de modo a equilibrar a ponte (V=0, no multímetro) e obter o valor de Rx.

O potenciômetro deve ser de precisão e graduado, para a leitura da resistência de medida (Rx).

Se utilizarmos R1=10*R2, poderemos medir valores de resistência bem superiores do que no caso em que R1=R2.

Analogamente se utilizarmos R1=R3/10, podemos medir valores de resistência bem menores, com mais precisão, do que no caso em que R1=R2.

CALIBRAÇÃO – Regressão Linear Simples

A calibração pode ser avaliada através de diferentes modelos matemáticos, ou estatísticos.  A regressão linear simples é um dos métodos que iremos utilizar. Tendo uma reta de referência, podemos avaliar se as outras medidas se aproximam dessa reta.  Quanto mais se aproximar, melhor será a calibração. 

MODELAMENTO MATEMÁTICO

Observe o exemplo abaixo, para um conjunto de medidas:

Os coeficientes de interesse são:

r = porcentagem de correlação linear (coeficiente);     ̶ 1 ≤ r ≤ 1

b = inclinação da reta

a = intersecção da reta

 

Construindo o gráfico com os resultados acima, tem-se:

Regressão Linear Simples

Introdução

            A análise de correlação e regressão compreende a análise de dados amostrais para saber se e como duas ou mais variáveis estão relacionadas uma com a outra numa população.

            A correlação mede a força, ou grau, de relacionamento entre duas variáveis; a regressão dá a equação que descreve o relacionamento em termos matemáticos.

            Os dados para análise de regressão e correlação provêm de (experimentos) observações de variáveis emparelhadas. Na regressão pressupõe-se alguma relação de causa e efeito, de explanação do comportamento entre as variáveis.

Ex. a temperatura e a resistência de um termistor NTC (Negative Temperature Coefficient); quantidade de poluentes e danos ecológicos.

Correlação Amostral

Serve para estudar o comportamento conjunto de duas variáveis quantitativas distintas.  Ou, em outras palavras, mede o grau de associação entre duas variáveis aleatórias x e y.

           

Para o estudo do comportamento conjunto de duas variáveis podem ser usados:

a) O diagrama de dispersão

Representação gráfica do conjunto de dados (pares de dados) em um sistema cartesiano.

Resumindo temos três situações:

            1) Se, quando uma das variáveis “cresce”, a outra, em média, também “cresce”, dizemos que entre as duas variáveis existe correlação positiva, tanto mais forte quanto mais perto de uma reta imaginária os pontos estiverem;

            2) Se, quando uma das variáveis “cresce”, a outra, em média, “decresce”, dizemos que entre as duas variáveis existe correlação negativa, tanto mais forte quanto mais perto de uma reta imaginária os pontos estiverem;

            3) Se os pontos estiverem dispersos, sem definição de direção, dizemos que a correlação é muito baixa, ou mesmo nula.  As variáveis nesse caso são ditas não correlacionadas.

b) O coeficiente de correlação

É um valor numérico, uma medida, para o grau de associação entre duas variáveis.

Se for observada uma associação entre as variáveis quantitativas (por exemplo, a partir de um diagrama de dispersão), é muito útil quantificar essa associabilidade.

Existem vários tipos de associação possíveis (exponencial, logarítmica, hiperbólica, parabólica, linear, etc.), aqui consideraremos apenas o tipo de relação mais simples: linear.   Julgaremos o quanto a nuvem de pontos do diagrama de dispersão se aproxima de uma reta.

           

Diagrama de Dispersão

Ao se plotar (“jogar”) num gráfico cartesiano os pares de informação referente a cada observação obtemos uma “nuvem” de pontos definidos pelas coordenadas x e y de cada ponto.  Essa nuvem, por sua vez, definirá um eixo ou direção que caracterizará o padrão de relacionamento entre x e y. A regressão será linear, quando observada tendência (ou eixo) linear na nuvem de pontos cartesianos.  A relação entre as variáveis será direta (ou positiva) quando os valores de y aumentarem em decorrência da elevação dos valores de x.  Será inversa (ou negativa) caso os valores de y variarem inversamente em relação aos de x. 

A figura-01 mostra o diagrama de dispersão referente às variáveis x e y.  Nota-se que existe uma relação direta entre as variáveis, ou seja, o aumento de y está diretamente ligado ao aumento de x.

Coeficiente de Correção Linear ou Coeficiente de Pearson (Karl Pearson, 1857- 1936)

r = mede o grau de relacionamento linear entre valores emparelhados x e y em uma amostra.

Mede a intensidade e a direção da relação linear entre duas variáveis quantitativas

Interpretando o Coeficiente de Correlação Linear

1)     O valor de ‘r’ sempre será um valor entre -1 ≤ r ≤ 1;

2)     Quanto mais próximo de –1: maior correlação negativa;

3)     Quanto mais próximo de 1: maior correlação positiva;

4)     Quanto mais próximo de 0:  menor a correlação linear.

Graficamente temos:

REGRESSÃO LINEAR SIMPLES

É o caso mais simples de regressão.  Temos duas variáveis e a relação entre elas é representada por uma reta.

Tem-se que:

Variável independente, ou variável explicativa (x); [manipulável].

Variável dependente, ou variável resposta (y); [observa o efeito]. 

Em linguagem coloquial: (y depende de x).

Em linguagem matemática: (y é função de x).

Em linguagem estatística: (Há regressão de y sobre x).

Valores de x são escolhidos e se observa uma correspondência y. 

O objetivo da regressão:

Avaliar uma possível dependência de y em relação à x.

Expressar esta relação por meio de uma equação de reta.

A reta da Regressão Linear:

Seja a equação y = a + bx a equação da reta, onde

            y = variável dependente;

            a = coeficiente linear (é o valor de y onde x = 0);

            b = coeficiente angular;

            x = variável independente.

Os pontos experimentais: y = a + bx +ε

ε = (diferença (=desvio) entre o valor observado e esperado de y)

  

OBTENÇÃO DA RETA DE REGRESSÃO:

Os dados necessários para obtenção da reta foram colocados na tabela:

Cálculo dos parâmetros para obtenção da reta:

Colocando a reta de regressão encontrada no gráfico original tem-se:

Relembrando a definição:

Dada uma coleção de dados amostrais emparelhados, a seguinte equação de regressão descreve a relação entre as duas variáveis:

O gráfico da equação é chamado reta de regressão (ou reta de melhor ajuste, ou reta de mínimos quadrados)

Desvio Padrão

O desvio padrão é um parâmetro estatístico que retrata a diferença entre os valores em relação a média e a dispersão entre as medidas.

Exercício-exemplo-1:

Para a tabela I, determine a média e o desvio padrão e dê a resposta de forma conveniente. A tabela com dados de medidas de estaturas de 10 pessoas.

Solução:

Calculando a média das alturas:

Calculando o desvio padrão:

Portanto, a resposta é:

Exercício-exemplo-2:

Para a tabela II, determine a média e o desvio padrão. 

Solução:

Distribuição normal, ou de Gauss (Gaussiana)

A distribuição Normal é uma das mais importantes distribuições contínuas de probabilidade, pois: Muitos fenômenos aleatórios comportam-se de forma próxima a essa distribuição.

Exemplos: altura e massa corporal, pressão sanguínea, dano ecológico de um rio, erro de medição, etc..

É definida pela seguinte função densidade de probabilidade:

Nota-se que, conhecendo a média e o desvio padrão consegue-se determinar qualquer probabilidade em uma distribuição normal.

Curva de distribuição Normal, ou curva de Gauss (Gaussiana).

A curva normal é simétrica em torno da média.

À medida que a curva se afasta da média, aproxima-se cada vez mais do eixo x, mas nunca o toca (pois a aproximação é assintótica).

Os pontos em que a curvatura muda são chamados pontos de inflexão.  Observa-se que o gráfico curva-se para baixo entre os pontos de inflexão e, para cima, à esquerda e à direita deles.

A área sob a curva totaliza 1 (100%).

Aproximadamente 0,68 (68%) dos valores de x situam-se entre os pontos (média – desvio padrão) e (média + desvio padrão).

Aproximadamente 0,95 (95%) dos valores de x estão entre os pontos (média – 2x desvio padrão) e (média + 2x desvio padrão).

Aproximadamente 0,997 (99,7%) dos valores de x estão entre os pontos (média – 3x desvio padrão) e (média + 3x desvio padrão).

METROLOGIA

Metrologia: É a ciência e estudo das medições.
Medir, entretanto, é uma atividade mais corriqueira do que parece. Ao olhar no relógio, por exemplo, você está vendo no mostrador o resultado de uma medição de tempo. Ao tomar um táxi, atravessar uma avenida, comprar um quilograma de mussarela no supermercado ou abastecer o carro no posto de gasolina, você presencia medições.

Mas o que é uma medição?

Medir é comparar uma grandeza com outra, de mesma natureza, tomada como padrão. Medição é, portanto, o conjunto de operações que tem por objetivo determinar o valor de uma grandeza.
Existe uma imensa gama de coisas diferentes que podem ser medidas sob vários aspectos. Cada um desses aspectos (comprimento, massa, volume) implica numa grandeza física diferente.

Algarismos significativos:

O resultado de uma medição expressa o valor de uma grandeza física. Os algarismos significativos são algarismos que têm importância na precisão no valor de uma medida. Tendo o resultado de uma medição, os algarismos significativos são todos aqueles contados, da esquerda para a direita, a partir do primeiro algarismo diferente de zero.

Exemplos-1:

5,67 → temos três algarismos significativos
5,6700 → temos cinco algarismos significativos, os zeros à direita dão mais precisão para o número.


Exemplos-2:

55,00
5555
555,5
0000,0005000

Exemplos acima têm quatro algarismos significativos.

Significados do zero, à esquerda e à direita. Zeros à esquerda do primeiro algarismo correto, antes ou depois da vírgula, não são significativos. Refletem apenas a utilização da unidade, ou seus múltiplos e submúltiplos.

Caso preferíssemos expressar o resultado 0,0595 m em centímetros, ao invés de metros, você escreveria 5,95 cm . Nada se altera, você continua com os mesmos três algarismos significativos.

Números com potência de dez (=notação científica), todos os algarismos são significativos, exceto a potência, vejamos:

567,8 = 5,678 x 10²  = 0,05678 x 10⁴  (quatro algarismos significativos). 

Os três números têm os algarismos 5678 seguidos, a potência de dez apenas move a vírgula, que não afeta a quantidade de algarismos significativos.

Algarismos duvidosos:

Vamos supor que você esteja efetuando a medição de um segmento de reta, utilizando para isso uma régua graduada em centímetros.

Você observa que o segmento de reta tem um pouco mais de quinze centímetros e menos que dezesseis centímetros. Então, você estima o valor deste "pouco" que ultrapassa quinze centímetros, expressando o resultado da medição assim: 15,7 centímetros.

Ou seja, você tem dois algarismos corretos (1 e 5) e um duvidoso (7), porque este último foi estimado por você - outro medidor poderia fazer uma estimativa diferente.

Em qualquer número que expressa uma medida, o algarismo duvidoso será o último algarismo significativo, contando da esquerda para direita.

Precisão em Operações Matemáticas

A Soma, Subtração, Multiplicação e Divisão sempre apresentam seus resultados como termos que apresentam a menor precisão.

Exemplos-1:

a)     1,2 + 1,31 = 2,51 → 2,5

b)     5,62 + 1,2 = 6,82 → 6,8

c)     6,813 + 1,11 = 7,923 → 7,92

d)    1,54 – 0,2 = 1,3 → 1,3

e)    1,66 – 0,11 = 1,55 → 1,55

f)     5,444 – 0,2 = 5,244 → 5,2

g)    2 x 2,1214 = 4,2428 → 4

h)    2,1 x 10,24 = 21,504 → 21,5

i)     2 / 1,12 = 1,7857142 → 1 ou 2

Precisão em medidas

Exemplos-2:

TIPOS DE ERROS

Sabe-se da metrologia que nenhuma medida é real. Mas, quanto mais medidas fizermos sobre o material, mais iremos nos aproximar da medida real do objeto.

Sendo assim, toda medida traz erros, sendo que os mesmos devem ser minimizados.

1) Erro sistemático

É um erro que se repete com certa constância, ou periodicidade. Como exemplo, podemos ter a falta de calibração do equipamento (equipamento não calibrado), medidas tomadas sem acuidade visual (erro de paralaxe).

2) Erro grosseiro

É um tipo de erro oriundo da falta de conhecimento, seja ato de medir ou da leitura errada da escala utilizada. Por exemplo: Dizer que o aro da bicicleta mede 70 km!

3) Erro aleatório

É um tipo de erro que não podemos ter total controle. Por exemplo: variações de temperatura em uma sala climatizada, pressão, pH, etc..

TRATAMENTO MATEMÁTICO

Em um conjunto de medidas podemos se aproximar do valor real (valor médio, média aritmética) e minimizar o erro (desvio médio das medidas em relação a média).

Exercício/Exemplo-1

Determinar a média e o desvio médio para um conjunto de 5 medidas de resistência elétrica.  Apresentar o resultado da seguinte forma:

Medidas:

R1 = 100,12Ω

R2 = 100,14Ω

R3 = 100,16Ω

R4 = 100,13Ω

R5 = 100,15Ω

d1 = 100,12 – 100,14 = - 0,02

d2 = 100,14 – 100,14 = 0

d3 = 100,16 – 100,14 = 0,02

d4 = 100,13 – 100,14 = - 0,01

d5 = 100,15 – 100,14 = 0,01

Exercício/Exemplo-2

Para o conjunto de dados da tabela I e II determinar:

a)     média;

b)     desvio médio;

c)      incerteza;

d)     indique a exatidão e precisão.

Lembrando que: A exatidão está associada à proximidade do valor verdadeiro e a precisão está associada à dispersão dos valores resultantes de uma série de medidas.

Tabela - I

d1 = 100,14 – 100,13 =  0,01

d2 = 100,11 – 100,13 =  -0,02

d3 = 100,14 – 100,13 =  0,01

d4 = 100,13 – 100,13 = 0,00

d5 = 100,11 – 100,13 =  -0,02

d6 = 100,15 – 100,13 = 0,02

d7 = 100,09 – 100,13 =  -0,04

d8 = 100,16 – 100,13 = 0,03

d9 = 100,12 – 100,13 =  -0,01

Tabela-II

d1 = 100,11 – 100,24 =  -0,13

d2 = 100,21 – 100,24 =  -0,03

d3 = 100,31 – 100,24 = 0,07

d4 = 100,41 – 100,24 = 0,17

d5 = 100,22 – 100,24 =  -0,02

d6 = 100,32 – 100,24 = 0,08

d7 = 100,42 – 100,24 = 0,18

d8 = 100,01 – 100,24 =  -0,23

d9 = 100,12 – 100,24 =  -0,12

PROPAGAÇÃO DE ERROS

Já sabemos que todas as medidas apresentam erros.  Esses erros podem ser acrescidos através das operações matemáticas utilizadas para identificar uma variável.

Vamos avaliar dois tipos de erros obtidos pela soma ou multiplicação.

SOMA:

Na soma, devemos somar as incertezas e os valores médios, separadamente.

MULTIPLICAÇÃO:

Na multiplicação, os valores médios são multiplicados e as incertezas são obtidas pela soma das razões das incertezas pelo valor médio individual.  Esse resultado deve ser multiplicado pelo produto das médias.

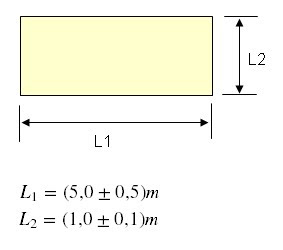
Exemplo:

Determinar o perímetro e a área para a figura abaixo.

Solução:

Perímetro (soma)

ÁREA (multiplicação)