Regressão Linear Simples

Introdução

            A análise de correlação e regressão compreende a análise de dados amostrais para saber se e como duas ou mais variáveis estão relacionadas uma com a outra numa população.

            A correlação mede a força, ou grau, de relacionamento entre duas variáveis; a regressão dá a equação que descreve o relacionamento em termos matemáticos.

            Os dados para análise de regressão e correlação provêm de (experimentos) observações de variáveis emparelhadas. Na regressão pressupõe-se alguma relação de causa e efeito, de explanação do comportamento entre as variáveis.

Ex. a temperatura e a resistência de um termistor NTC (Negative Temperature Coefficient); quantidade de poluentes e danos ecológicos.

Correlação Amostral

Serve para estudar o comportamento conjunto de duas variáveis quantitativas distintas.  Ou, em outras palavras, mede o grau de associação entre duas variáveis aleatórias x e y.

           

Para o estudo do comportamento conjunto de duas variáveis podem ser usados:

a) O diagrama de dispersão

Representação gráfica do conjunto de dados (pares de dados) em um sistema cartesiano.

Resumindo temos três situações:

            1) Se, quando uma das variáveis “cresce”, a outra, em média, também “cresce”, dizemos que entre as duas variáveis existe correlação positiva, tanto mais forte quanto mais perto de uma reta imaginária os pontos estiverem;

            2) Se, quando uma das variáveis “cresce”, a outra, em média, “decresce”, dizemos que entre as duas variáveis existe correlação negativa, tanto mais forte quanto mais perto de uma reta imaginária os pontos estiverem;

            3) Se os pontos estiverem dispersos, sem definição de direção, dizemos que a correlação é muito baixa, ou mesmo nula.  As variáveis nesse caso são ditas não correlacionadas.

b) O coeficiente de correlação

É um valor numérico, uma medida, para o grau de associação entre duas variáveis.

Se for observada uma associação entre as variáveis quantitativas (por exemplo, a partir de um diagrama de dispersão), é muito útil quantificar essa associabilidade.

Existem vários tipos de associação possíveis (exponencial, logarítmica, hiperbólica, parabólica, linear, etc.), aqui consideraremos apenas o tipo de relação mais simples: linear.   Julgaremos o quanto a nuvem de pontos do diagrama de dispersão se aproxima de uma reta.

           

Diagrama de Dispersão

Ao se plotar (“jogar”) num gráfico cartesiano os pares de informação referente a cada observação obtemos uma “nuvem” de pontos definidos pelas coordenadas x e y de cada ponto.  Essa nuvem, por sua vez, definirá um eixo ou direção que caracterizará o padrão de relacionamento entre x e y. A regressão será linear, quando observada tendência (ou eixo) linear na nuvem de pontos cartesianos.  A relação entre as variáveis será direta (ou positiva) quando os valores de y aumentarem em decorrência da elevação dos valores de x.  Será inversa (ou negativa) caso os valores de y variarem inversamente em relação aos de x. 

A figura-01 mostra o diagrama de dispersão referente às variáveis x e y.  Nota-se que existe uma relação direta entre as variáveis, ou seja, o aumento de y está diretamente ligado ao aumento de x.

Coeficiente de Correção Linear ou Coeficiente de Pearson (Karl Pearson, 1857- 1936)

r = mede o grau de relacionamento linear entre valores emparelhados x e y em uma amostra.

Mede a intensidade e a direção da relação linear entre duas variáveis quantitativas

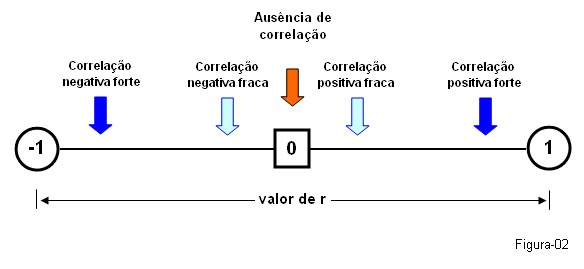
Interpretando o Coeficiente de Correlação Linear

1)     O valor de ‘r’ sempre será um valor entre -1 ≤ r ≤ 1;

2)     Quanto mais próximo de –1: maior correlação negativa;

3)     Quanto mais próximo de 1: maior correlação positiva;

4)     Quanto mais próximo de 0:  menor a correlação linear.

Graficamente temos:

REGRESSÃO LINEAR SIMPLES

É o caso mais simples de regressão.  Temos duas variáveis e a relação entre elas é representada por uma reta.

Tem-se que:

Variável independente, ou variável explicativa (x); [manipulável].

Variável dependente, ou variável resposta (y); [observa o efeito]. 

Em linguagem coloquial: (y depende de x).

Em linguagem matemática: (y é função de x).

Em linguagem estatística: (Há regressão de y sobre x).

Valores de x são escolhidos e se observa uma correspondência y. 

O objetivo da regressão:

Avaliar uma possível dependência de y em relação à x.

Expressar esta relação por meio de uma equação de reta.

A reta da Regressão Linear:

Seja a equação y = a + bx a equação da reta, onde

            y = variável dependente;

            a = coeficiente linear (é o valor de y onde x = 0);

            b = coeficiente angular;

            x = variável independente.

Os pontos experimentais: y = a + bx +ε

ε = (diferença (=desvio) entre o valor observado e esperado de y)

  

OBTENÇÃO DA RETA DE REGRESSÃO:

Os dados necessários para obtenção da reta foram colocados na tabela:

Cálculo dos parâmetros para obtenção da reta:

Colocando a reta de regressão encontrada no gráfico original tem-se:

Relembrando a definição:

Dada uma coleção de dados amostrais emparelhados, a seguinte equação de regressão descreve a relação entre as duas variáveis:

O gráfico da equação é chamado reta de regressão (ou reta de melhor ajuste, ou reta de mínimos quadrados)