O desvio padrão é um parâmetro estatístico que retrata a
diferença entre os valores em relação a média e a dispersão entre as medidas.
Exercício-exemplo-1:
Para a tabela I, determine a média e o desvio padrão e dê a
resposta de forma conveniente. A tabela com dados de medidas de estaturas de 10 pessoas.
Solução:
Calculando a média das alturas:
Calculando o desvio padrão:
Portanto, a resposta é:
Exercício-exemplo-2:
Para a tabela II, determine a média e o desvio padrão.
Solução:
Distribuição normal,
ou de Gauss (Gaussiana)
A distribuição Normal é uma das mais importantes
distribuições contínuas de probabilidade, pois: Muitos fenômenos aleatórios
comportam-se de forma próxima a essa distribuição.
Exemplos: altura e massa corporal, pressão sanguínea, dano
ecológico de um rio, erro de medição, etc..
É definida pela seguinte função densidade de
probabilidade:
Nota-se que, conhecendo a média e o desvio padrão
consegue-se determinar qualquer probabilidade em uma distribuição normal.
Curva de distribuição
Normal, ou curva de Gauss (Gaussiana).
A curva normal é simétrica em torno da média.
À medida que a curva se afasta da média, aproxima-se cada
vez mais do eixo x, mas nunca o toca (pois a aproximação é assintótica).
Os pontos em que a curvatura muda são chamados pontos de
inflexão. Observa-se que o gráfico
curva-se para baixo entre os pontos de inflexão e, para cima, à esquerda e à
direita deles.
A área sob a curva totaliza 1 (100%).
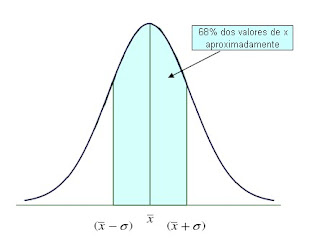
Aproximadamente 0,68 (68%) dos valores de x situam-se entre
os pontos (média – desvio padrão) e (média + desvio padrão).
Aproximadamente 0,95 (95%) dos valores de x estão entre os
pontos (média – 2x desvio padrão) e (média + 2x desvio padrão).
Aproximadamente 0,997 (99,7%) dos valores de x estão entre
os pontos (média – 3x desvio padrão) e (média + 3x desvio padrão).










Nenhum comentário:
Postar um comentário